三个素性检验

Python实现三个素性检验

使用方法：

直接运行，根据提示选择模式、输入检验的数n和循环次数k即可

代码

import random
import time

def QuickPower(a,n,p):#快速幂算法
   tmp = a
   ret =1
   while(n >0):
       if(n&1):
           ret = (ret * tmp) % p
       tmp = (tmp * tmp) % p
       n>>=1
   return ret
def Jacobi(n,m):# calc Jacobi(n/m)
   n = n%m
   if n==0:
       return 0
   Jacobi2 =1
   if not(n&1):#若有n为偶数,计算Jacobi2 = Jacobi(2/m)^(s)其中n = 2^s*t t为奇数
       k = (-1)**(((m**2-1)//8)&1)
       while not(n&1):
           Jacobi2 *= k
           n >>=1
   if n==1:
       return Jacobi2
   return Jacobi2 * (-1)**(((m-1)//2*(n-1)//2)&1) * Jacobi(m%n,n)

def Exgcd(r0,r1):# calc ax+by = gcd(a, b) return x
   x0,y0 =1,0
   x1,y1 =0,1
   x,y = r0,r1
   r = r0 % r1
   q = r0 // r1
   while r:
       x,y = x0 - q * x1,y0 - q * y1
       x0,y0 = x1,y1
       x1,y1 = x,y
       r0 = r1
       r1 = r
       r = r0 % r1
       q = r0 // r1
   return x

def Fermat(x,T):# Fermat素性判定
       if x <2:
               return False
       if x<=3:
               return True
       if x%2==0 or x%3==0:
               return False
       for i in range(T):
               ran = random.randint(2,x-2)#随机取[2, x-2]的一个整数
               if QuickPower(ran,x-1,x) !=1:
                       return False
       return True

def Solovay_Stassen(x,T):# Solovay_Stassen素性判定
   if x <2:
       return False
   if x <=3:
       return True
   if x%2==0 or x%3==0:
       return False
   for i in range(T):#随机选择T个整数
       ran = random.randint(2,x-2)
       r = QuickPower(ran,(x-1)//2,x)
       if r !=1 and r != x-1:
           return False
       if r == x-1:
           r = -1
       if r != Jacobi(ran,x):
           return False
   return True
def MillerRabin(x,ran):# x-1 = 2^s*t
   tx = x-1
   s2 = tx&(~tx+1)#取出最后一位以1开头的二进制 即2^s
   r = QuickPower(ran,tx//s2,x)
   if r ==1 or r == tx:
       return True
   while s2>1:#从2^s -> 2^1循环s次
       r = (r*r)%x
       if r ==1:
           return False
       if r == tx:
           return True
       s2 >>=1
   return False
def MillerRabin_init(x,T):#Miller-Rabin素性判定
   if x <2:
       return False
   if x <=3:
       return True
   if x%2==0 or x%3==0:
       return False
   for i in range(T):#随机选择T个整数
       ran = random.randint(2,x-2)
       if not MillerRabin(x,ran):
           return False
   return True
def CRT(b,m,n):# calc x = b[] % m[]
   M =1
   for i in range(n):
       M *= m[i]
   ans =0
   for i in range(n):
       ans += b[i] * M // m[i] * Exgcd(M//m[i],m[i])
   return ans%M

if __name__ == "__main__":
    print('1 ：费马素性检验\n2 : Solovay_Stassen素性检验\n3 : 米勒.拉宾素性检验\n4 : 三个素性检验一起进行\n')
    cho=input('选择运行模式：')
    if cho!='1'and cho!='2'and cho!='3'and cho!='4' :
        print('输入错误！！')
        exit()   
    n = int(input("请输入需要检测的整数n："))
    k = int(input("请输入循环次数k："))
    print('*'*100)
    if cho=='1':
        a=Fermat(n,k)
        print('费马素性检验结果：',a)
    elif cho=='2':
        b=Solovay_Stassen(n,k)
        print('Solovay_Stassen素性检验结果：',b)
    elif cho=='3':
        c=MillerRabin_init(n,k)
        print('米勒.拉宾素性检验结果：',c)
    elif cho=='4':
        start = time.perf_counter()
        a=Fermat(n,k)
        end = time.perf_counter()
        print('费马素性检验结果：',a)
        print("费马素性检验运行耗时",end-start)
        print('\n')

        start = time.perf_counter()
        b=Solovay_Stassen(n,k)
        end = time.perf_counter()
        print('Solovay_Stassen素性检验结果：',b)
        print("Solovay_Stassen素性检验运行耗时",end-start)
        print('\n')

        start = time.perf_counter()
        c=MillerRabin_init(n,k)
        end = time.perf_counter()
        print('米勒.拉宾素性检验结果：',c)
        print("米勒.拉宾素性检验运行耗时",end-start)
    

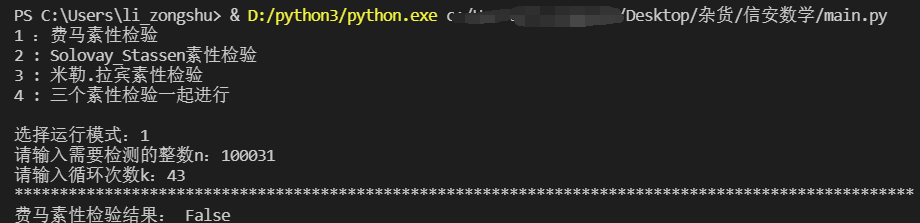
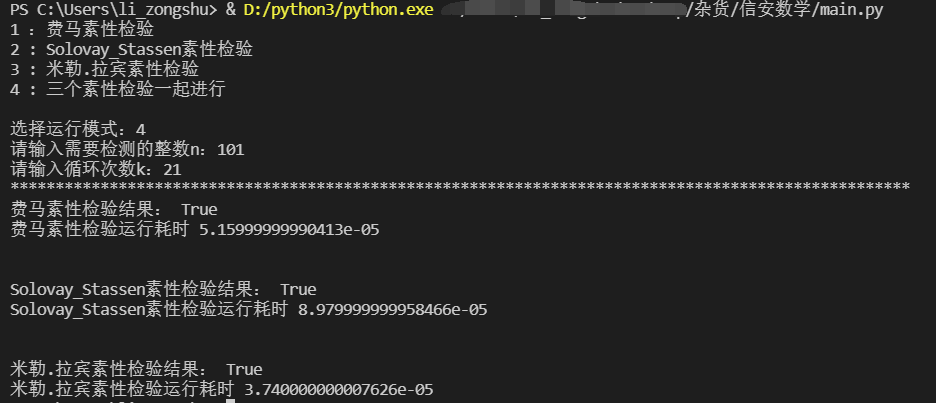
运行效果